我们规定:若点O是线段MN的中点,则称点M关于O的对称点是N(或称点M与点N关于O成中心对称);若直线n是线段MN的垂直平分线,则称点M关于n的对称点是N(或称点M与点N关于n成轴对称),如图现有石头A和石头B关于竹竿l对称,石头A和石头B相距80cm一只电子青蛙位于点P,与石头A相距60cm,与竹竿l相距30cm,他按照如下指令跳动:第一跳落点于P1,P与P1关于点A成中心对称;第二跳落点于P2,P2与P1关于竹竿l成轴对称;第三跳落点于P3,P3与P2关于点B成中心对称;第四跳落点于P4,P4与P3关于竹竿l成轴对称;以此跃下去,若每25跳可以休息一次.
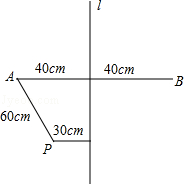
(1)画出这只电子青蛙前四跳运动的路线图,并求点P4与点P1的距离(不须说明理由)
(2)求电子青蛙第三次休息点与点P的距离.