（本小题满分12分）
如图1，在三棱锥P－A.BC中，PA.⊥平面A.BC，A.C⊥BC，D为侧棱PC上一点，它的正(主)视图和侧(左)视图如图2所示．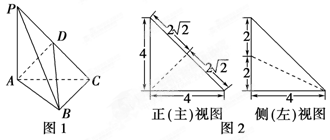
(1) 证明：A.D⊥平面PBC；
(2) 求三棱锥D－A.BC的体积；
(3) 在∠A.CB的平分线上确定一点Q，使得PQ∥平面A.BD，并求此时PQ的长．
相关试题
分）已知函数
．
与
,
与
;
与
有什么关系？并证明你的结论;
的值 ．
分）
．
的最大值及相应的
的值.
的定义域为
,
,求
的取值范围；
的最大值与最小值，并求出最值时对应的
的值．
。 
的定义域；
向直线
作垂线，垂足为
.求直线推荐套卷
（本小题满分12分）
如图1，在三棱锥P－A.BC中，PA.⊥平面A.BC，A.C⊥BC，D为侧棱PC上一点，它的正(主)视图和侧(左)视图如图2所示．
(1) 证明：A.D⊥平面PBC；
(2) 求三棱锥D－A.BC的体积；
(3) 在∠A.CB的平分线上确定一点Q，使得PQ∥平面A.BD，并求此时PQ的长．
粤公网安备 44130202000953号