(本小题满分13分)
某工厂去年的某产品的年销售量为100万只,每只产品的销售价为10元,每只产品固定成本为8元.今年,工厂第一次投入100万元(科技成本),并计划以后每年比上一年多投入100万元(科技成本),预计销售量从今年开始每年比上一年增加10万只,第n次投入后,每只产品的固定成本为 (
(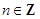 且n≥0),若产品销售价保持不变,第n次投入后的年利润为
且n≥0),若产品销售价保持不变,第n次投入后的年利润为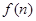 万元.
万元.
(Ⅰ)求出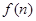 的表达式;
的表达式;
(Ⅱ)若今年是第1年,问第几年年利润最高?最高利润为多少万元?
推荐套卷
(本小题满分13分)
某工厂去年的某产品的年销售量为100万只,每只产品的销售价为10元,每只产品固定成本为8元.今年,工厂第一次投入100万元(科技成本),并计划以后每年比上一年多投入100万元(科技成本),预计销售量从今年开始每年比上一年增加10万只,第n次投入后,每只产品的固定成本为 (
(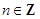 且n≥0),若产品销售价保持不变,第n次投入后的年利润为
且n≥0),若产品销售价保持不变,第n次投入后的年利润为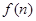 万元.
万元.
(Ⅰ)求出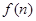 的表达式;
的表达式;
(Ⅱ)若今年是第1年,问第几年年利润最高?最高利润为多少万元?