如图,一个机器人从O点出发,向正东方向走3米到达A1点,再向正北方向走6米到达A2点,再向正西方向走9米到达A3点,再向正南方向走12米到达A4点,再向正东方向走15米到达A5点,按如此规律走下去,当机器人走到A6点时,A6点的坐标是________.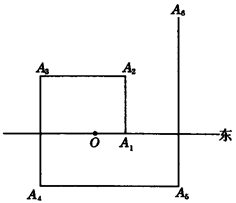
如图,一个机器人从O点出发,向正东方向走3米到达A1点,再向正北方向走6米到达A2点,再向正西方向走9米到达A3点,再向正南方向走12米到达A4点,再向正东方向走15米到达A5点,按如此规律走下去,当机器人走到A6点时,A6点的坐标是________.