（本小题满分12分）为了调查甲、乙两个交通站的车流量，随机选取了14天，统计每天上午8∶00~12∶00间各自的车流量（单位：百辆），得如图所示的统计图，试求：
（1）甲、乙两个交通站的车流量的极差分别是多少？
（2）甲交通站的车流量在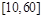
间的频率是多少？
（3）甲、乙两个交通站哪个站更繁忙？并说明理由.
相关试题
中，内角
对边的边长分别是
，已知
，
．
，求
；（2）若
，求
面积．
中，
的值.（2）求
的值。
中，
，且
成等比数列，求数列
.
，
，
, 
为等差数列{an}的前n项和，
,
，求
.
中，若
求首项
和公比
。推荐套卷
（本小题满分12分）为了调查甲、乙两个交通站的车流量，随机选取了14天，统计每天上午8∶00~12∶00间各自的车流量（单位：百辆），得如图所示的统计图，试求：
（1）甲、乙两个交通站的车流量的极差分别是多少？
（2）甲交通站的车流量在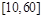间的频率是多少？
（3）甲、乙两个交通站哪个站更繁忙？并说明理由.
粤公网安备 44130202000953号