如图,△ABC中,以BC为直径的圆交AB于点D,∠ACD=∠ABC.
(1)求证:CA是圆的切线;
(2)若点E是BC上一点,已知BE=6,tan∠ABC=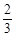 ,tan∠AEC=
,tan∠AEC=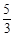 ,求圆的直径.
,求圆的直径.
相关知识点
推荐套卷
如图,△ABC中,以BC为直径的圆交AB于点D,∠ACD=∠ABC.
(1)求证:CA是圆的切线;
(2)若点E是BC上一点,已知BE=6,tan∠ABC=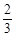 ,tan∠AEC=
,tan∠AEC=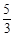 ,求圆的直径.
,求圆的直径.