某特技飞行队在名胜风景旅游区——张家界天门洞特技表演, 其中一架飞机起飞后的高度变化如下表:(本题7分)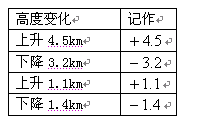
(1)此时这架飞机比起飞点高了多少千米?
(2)如果飞机每上升或下降1 km需消耗2L燃油,那么这架飞机在这4个动作表演过程中,一共消耗了多少升燃油?
(3)如果飞机做特技表演时,有4个规定动作,前3个动作起飞后高度变化如下:上升3.8km,下降2.9km,再上升1.6km,若要使飞机最终比起飞点高出1km,问第4个动作是上升还是下降,上升或下降多少千米?
相关知识点
推荐套卷
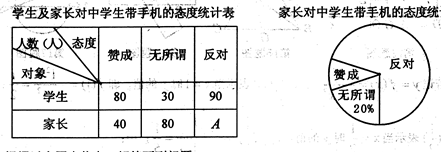
 1)统计表中的A=_▲;
1)统计表中的A=_▲; 家长“赞成”的圆心角的度数为_▲度;
家长“赞成”的圆心角的度数为_▲度;
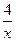 的图象与一次函数y
的图象与一次函数y -2sin60º+|-1|;
-2sin60º+|-1|;
 过点P, P点的坐标为(3-m,
过点P, P点的坐标为(3-m, 的解,PA⊥x轴于点A,PB⊥y轴于点B.
的解,PA⊥x轴于点A,PB⊥y轴于点B.

 粤公网安备 44130202000953号
粤公网安备 44130202000953号