（本小题满分12分）已知△BCD中，∠BCD＝90°，BC＝CD＝1，AB⊥平面BCD，∠ADB＝60°，E，F分别是AC，AD上的动点，且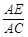
＝
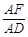＝λ (0＜λ＜1)．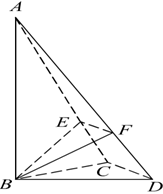
（1）求证：不论λ为何值，总有平面BEF⊥平面ABC；
（2）当λ为何值时？平面BEF⊥平面ACD.
推荐套卷
（本小题满分12分）已知△BCD中，∠BCD＝90°，BC＝CD＝1，AB⊥平面BCD，∠ADB＝60°，E，F分别是AC，AD上的动点，且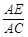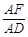＝＝λ (0＜λ＜1)．
（1）求证：不论λ为何值，总有平面BEF⊥平面ABC；
（2）当λ为何值时？平面BEF⊥平面ACD.
粤公网安备 44130202000953号