已知二次函数y=-x2+4x+5，完成下列各题：
（1）将函数关系式用配方法化为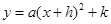
的形式，并写出它的顶点坐标、对称轴.
（2）求出它的图象与坐标轴的交点坐标.
（3）在直角坐标系中，画出它的图象.
（4）根据图象说明：当x为何值时，y>0；当x为何值时，y<0.
相关试题
与
相等，OD⊥BC，OE⊥AC，垂足分别为D、E，且OD=OE，那么△ABC是什么三角形，为什么？
相关知识点
推荐套卷
已知二次函数y=-x2+4x+5，完成下列各题：
（1）将函数关系式用配方法化为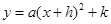的形式，并写出它的顶点坐标、对称轴.
（2）求出它的图象与坐标轴的交点坐标.
（3）在直角坐标系中，画出它的图象.
（4）根据图象说明：当x为何值时，y>0；当x为何值时，y<0.
粤公网安备 44130202000953号