如图，隧道的横截面由抛物线和长方形构成，长方形的长是8m，宽是2m，抛物线的解析式为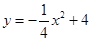
。
（1）一辆货运车车高4m，宽2m，它能通过该隧道吗？
（2）如果该隧道内设双行道，中间遇车间隙为0.4m，那么这辆卡车是否可以通过？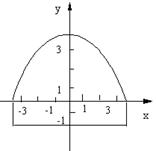
，求 ∠4的度数
与x2 +bx-1的和中不存在含x的一次项，求b的值
相关知识点
推荐套卷
如图，隧道的横截面由抛物线和长方形构成，长方形的长是8m，宽是2m，抛物线的解析式为。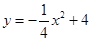
（1）一辆货运车车高4m，宽2m，它能通过该隧道吗？
（2）如果该隧道内设双行道，中间遇车间隙为0.4m，那么这辆卡车是否可以通过？
粤公网安备 44130202000953号