(本大题13分)已知函数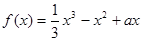 (
(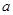 为常数)
为常数)
(1)若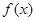 在区间
在区间 上单调递减,求
上单调递减,求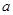 的取值范围;
的取值范围;
(2)若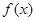 与直线
与直线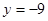 相切:
相切:
(ⅰ)求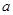 的值;
的值;
(ⅱ)设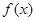 在
在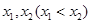 处取得极值,记点M (
处取得极值,记点M ( ,
,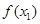 ),N(
),N(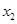 ,
,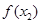 ),P(
),P(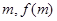 ),
), 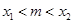 , 若对任意的m
, 若对任意的m 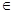 (
( , x
, x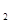 ),线段MP与曲线f(x)均有异于M,P的公共点,试确定
),线段MP与曲线f(x)均有异于M,P的公共点,试确定 的最小值,并证明你的结论.
的最小值,并证明你的结论.
相关知识点
推荐套卷
(本大题13分)已知函数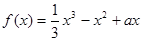 (
(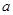 为常数)
为常数)
(1)若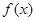 在区间
在区间 上单调递减,求
上单调递减,求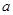 的取值范围;
的取值范围;
(2)若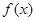 与直线
与直线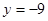 相切:
相切:
(ⅰ)求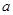 的值;
的值;
(ⅱ)设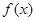 在
在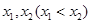 处取得极值,记点M (
处取得极值,记点M ( ,
,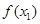 ),N(
),N(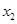 ,
,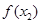 ),P(
),P(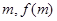 ),
), 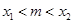 , 若对任意的m
, 若对任意的m 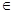 (
( , x
, x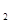 ),线段MP与曲线f(x)均有异于M,P的公共点,试确定
),线段MP与曲线f(x)均有异于M,P的公共点,试确定 的最小值,并证明你的结论.
的最小值,并证明你的结论.