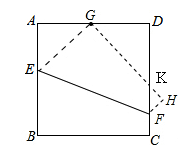
如图,矩形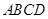 中,
中,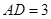 厘米,
厘米, 厘米(
厘米( ).动点
).动点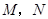 同时从
同时从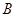 点出发,分别沿
点出发,分别沿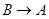 ,
,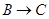 运动,速度是
运动,速度是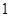 厘米/秒.过
厘米/秒.过 作直线垂直于
作直线垂直于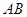 ,分别交
,分别交 ,
,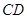 于
于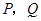 .当点
.当点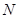 到达终点
到达终点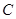 时,点
时,点 也随之停止运动.设运动时间为
也随之停止运动.设运动时间为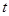 秒.
秒.
(1)若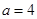 厘米,
厘米,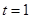 秒,则
秒,则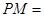 ______厘米;
______厘米;
(2)若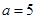 厘米,求时间
厘米,求时间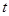 ,使
,使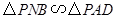 ,并求出它们的相似比;
,并求出它们的相似比;
(3)若在运动过程中,存在某时刻使梯形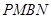 与梯形
与梯形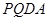 的面积相等,求
的面积相等,求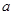 的取值范围;
的取值范围;
(4)是否存在这样的矩形:在运动过程中,存在某时刻使梯形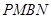 ,梯形
,梯形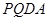 ,梯形
,梯形 的面积都相等?若存在,求
的面积都相等?若存在,求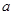 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.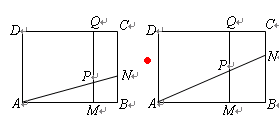
相关知识点
推荐套卷
 、
、 、
、 ,求△ABC的面积.
,求△ABC的面积.
 、
、 的格点△DEF;
的格点△DEF; ,PR=
,PR= ,求六边形AQRDEF的面积.
,求六边形AQRDEF的面积.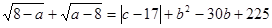 ,
,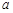 ,b,c的值;
,b,c的值;
 B点,然后再沿北偏西30°方向走了500m到达目的地C点.
B点,然后再沿北偏西30°方向走了500m到达目的地C点.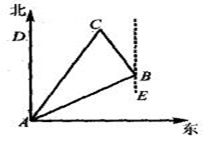
 粤公网安备 44130202000953号
粤公网安备 44130202000953号