设双曲线C：
－y2＝1的左、右顶点分别为A1、A2，垂直于x轴的直线m与双曲线C交于不同的两点P、Q．
（1）若直线m与x轴正半轴的交点为T，且
·
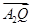＝1，求点T的坐标；
（2）求直线A1P与直线A2Q的交点M的轨迹E的方程；
（3）过点F（1，0）作直线l与（2）中的轨迹E交于不同的两点A、B，设
＝λ·
，若λ∈[－2，－1]，求|
＋
|（T为（1）中的点）的取值范围．
＜0 （a∈R）.
，求关于x的不等式(a-3b)x+(b-2a)＞0的解集.
＞0;(2)9x2-6x+1≥0.
＞0 (a∈R).
≥
(x2-9)-3x.相关知识点
推荐套卷
设双曲线C：－y2＝1的左、右顶点分别为A1、A2，垂直于x轴的直线m与双曲线C交于不同的两点P、Q．
（1）若直线m与x轴正半轴的交点为T，且·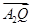＝1，求点T的坐标；
（2）求直线A1P与直线A2Q的交点M的轨迹E的方程；
（3）过点F（1，0）作直线l与（2）中的轨迹E交于不同的两点A、B，设＝λ·，若λ∈[－2，－1]，求|＋|（T为（1）中的点）的取值范围．
粤公网安备 44130202000953号