在科技馆里,小亮看见一台名为帕斯卡三角的仪器,如图所示,当一实心小球从入口落下,它在依次碰到每层菱形挡块时,会等可能地向左或向右落下.
(1)试问小球通过第二层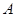 位置的概率是多少?
位置的概率是多少?
(2)请用学过的数学方法模拟试验,并具体说明小球下落到第三层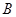 位置和第四层
位置和第四层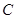
位置处的概率各是多少?
相关知识点
推荐套卷
在科技馆里,小亮看见一台名为帕斯卡三角的仪器,如图所示,当一实心小球从入口落下,它在依次碰到每层菱形挡块时,会等可能地向左或向右落下.
(1)试问小球通过第二层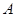 位置的概率是多少?
位置的概率是多少?
(2)请用学过的数学方法模拟试验,并具体说明小球下落到第三层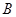 位置和第四层
位置和第四层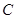
位置处的概率各是多少?