(本小题满分14分)
如图,在半径为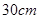 的
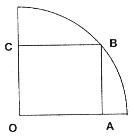
的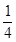 圆形(O为圆心)铝皮上截取一块矩形材料OABC,其中点B在圆弧上,点A、C在两半径上,现将此矩形铝皮OABC卷成一个以AB为母线的圆柱形罐子的侧面(不计剪裁和拼接损耗),设矩形的边长
圆形(O为圆心)铝皮上截取一块矩形材料OABC,其中点B在圆弧上,点A、C在两半径上,现将此矩形铝皮OABC卷成一个以AB为母线的圆柱形罐子的侧面(不计剪裁和拼接损耗),设矩形的边长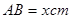 ,圆柱的体积为
,圆柱的体积为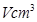 .
.
(1)写出体积V关于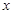 的函数关系式;
的函数关系式;
(2)当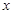 为何值时,才能使做出的圆柱形罐子体积V最大?
为何值时,才能使做出的圆柱形罐子体积V最大?
推荐套卷
(本小题满分14分)
如图,在半径为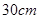 的
的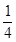 圆形(O为圆心)铝皮上截取一块矩形材料OABC,其中点B在圆弧上,点A、C在两半径上,现将此矩形铝皮OABC卷成一个以AB为母线的圆柱形罐子的侧面(不计剪裁和拼接损耗),设矩形的边长
圆形(O为圆心)铝皮上截取一块矩形材料OABC,其中点B在圆弧上,点A、C在两半径上,现将此矩形铝皮OABC卷成一个以AB为母线的圆柱形罐子的侧面(不计剪裁和拼接损耗),设矩形的边长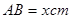 ,圆柱的体积为
,圆柱的体积为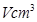 .
.
(1)写出体积V关于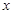 的函数关系式;
的函数关系式;
(2)当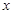 为何值时,才能使做出的圆柱形罐子体积V最大?
为何值时,才能使做出的圆柱形罐子体积V最大?