如图,在平行四边形ABCD中,∠BAD=32°.分别以BC、CD为边向外作△BCE和△DCF,使BE=BC,DF=DC,∠EBC=∠CDF,延长AB交边EC于点H,点H在E、C两点之间,连结AE、AF.
(1)求证:△ABE≌△FDA.
(2)当AE⊥AF时,求∠EBH的度数.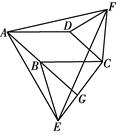
相关知识点
推荐套卷
如图,在平行四边形ABCD中,∠BAD=32°.分别以BC、CD为边向外作△BCE和△DCF,使BE=BC,DF=DC,∠EBC=∠CDF,延长AB交边EC于点H,点H在E、C两点之间,连结AE、AF.
(1)求证:△ABE≌△FDA.
(2)当AE⊥AF时,求∠EBH的度数.