已知函数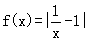
（Ⅰ）判断f(x)在
上的单调性，并证明你的结论；
（Ⅱ）若集合A="{y" | y=f(x)，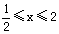
}，B=[0,1]， 试判断A与B的关系；
（Ⅲ）若存在实数a、b(a<b)，使得集合{y | y=f(x)，a≤x≤b}=[ma，mb]，求非零实数m的取值范围.
，
，是否存在实数
，使
？若存在，求出
，
是
的必要不充分条件。
，设
：函数
在
上单调递减，
：曲线
与
轴交于不同的两点。如果
和
的取值范围。
，试问：（1）当
时，
是真命题吗？（2）
是真命题吗？
。相关知识点
推荐套卷
已知函数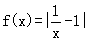
（Ⅰ）判断f(x)在上的单调性，并证明你的结论；
（Ⅱ）若集合A="{y" | y=f(x)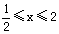，}，B=[0,1]， 试判断A与B的关系；
（Ⅲ）若存在实数a、b(a<b)，使得集合{y | y=f(x)，a≤x≤b}=[ma，mb]，求非零实数m的取值范围.
粤公网安备 44130202000953号