(满分12分)某次体能测试中，规定每名运动员一开始就要参加且最多参加四次测试.一旦测试通过,就不再参加余下的测试,否则一直参加完四次测试为止.已知运动员甲的每次通过率为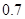
(假定每次通过率相同).
(1) 求运动员甲最多参加两次测试的概率;
(2) 求运动员甲参加测试的次数的分布列及数学期望(精确到0.1).
相关试题
．
，求函数
在
上的最大值和最小值；
中至少有一个极值点，求
的取值范围．
，曲线
在
．
时，函数
有极值，求函数
，求
的单调递增区间（其中
）．
=
（a＞1）．
＞
在闭区间
的最大值记为
．
，求出
的取值范围．
的前
项和为
,且对任意正整数
是
为等比数列；推荐套卷
(满分12分)某次体能测试中，规定每名运动员一开始就要参加且最多参加四次测试.一旦测试通过,就不再参加余下的测试,否则一直参加完四次测试为止.已知运动员甲的每次通过率为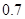(假定每次通过率相同).
(1) 求运动员甲最多参加两次测试的概率;
(2) 求运动员甲参加测试的次数的分布列及数学期望(精确到0.1).
粤公网安备 44130202000953号