（本小题满分12分）
如图，在几何体P－ABCD中，四边形ABCD为矩形，PA⊥平面ABCD，AB＝PA＝2.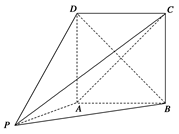
(1)当AD＝2时，求证：平面PBD⊥平面PAC；
(2)若PC与AD所成角为45°，求几何体P－ABCD的体积．
相关试题
是公差不为零的等差数列，
，且
成等比数列.
,求数列
的前n项和
.
为等差数列，
，其前n项和为
，若
，
值.
的内角
的对边分别为
，若
，且
，求
和
﹒
；（2）
．
；
，求Tn的最大值及此时n的值.相关知识点
推荐套卷
（本小题满分12分）
如图，在几何体P－ABCD中，四边形ABCD为矩形，PA⊥平面ABCD，AB＝PA＝2.
(1)当AD＝2时，求证：平面PBD⊥平面PAC；
(2)若PC与AD所成角为45°，求几何体P－ABCD的体积．
粤公网安备 44130202000953号