.已知 为常数,函数
为常数,函数 (
( )。
)。
(Ⅰ) 若函数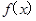 在区间(-2,-1)上为减函数,求实数
在区间(-2,-1)上为减函数,求实数 的取值范围;
的取值范围;
(Ⅱ).设  记函数
记函数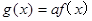 ,已知函数
,已知函数 在区间
在区间 内有两个极值点
内有两个极值点 ,且
,且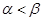 ,若对于满足条件的任意实数
,若对于满足条件的任意实数 都有
都有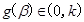 (
( 为正整数),求
为正整数),求 的最小值。
的最小值。
推荐套卷
.已知 为常数,函数
为常数,函数 (
( )。
)。
(Ⅰ) 若函数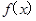 在区间(-2,-1)上为减函数,求实数
在区间(-2,-1)上为减函数,求实数 的取值范围;
的取值范围;
(Ⅱ).设  记函数
记函数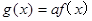 ,已知函数
,已知函数 在区间
在区间 内有两个极值点
内有两个极值点 ,且
,且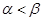 ,若对于满足条件的任意实数
,若对于满足条件的任意实数 都有
都有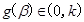 (
( 为正整数),求
为正整数),求 的最小值。
的最小值。