某射击运动员为争取获得2010年广州亚运会的参赛资格正在加紧训练.已知在某次训练中他射击了 枪,每一枪的射击结果相互独立,每枪成绩不低于10环的概率为
枪,每一枪的射击结果相互独立,每枪成绩不低于10环的概率为 ,设
,设 为本次训练中成绩不低于10环的射击次数,
为本次训练中成绩不低于10环的射击次数, 的数学期望
的数学期望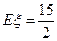 ,方差
,方差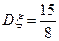 .
.
(1)求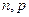 的值;
的值;
(2)训练中教练要求:若有5枪或5枪以上成绩低于10环,则需要补射,求该运动员在本次训练中需要补射的概率.
(结果用分数表示.已知: ,
,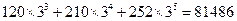 )
)
相关知识点
推荐套卷
某射击运动员为争取获得2010年广州亚运会的参赛资格正在加紧训练.已知在某次训练中他射击了 枪,每一枪的射击结果相互独立,每枪成绩不低于10环的概率为
枪,每一枪的射击结果相互独立,每枪成绩不低于10环的概率为 ,设
,设 为本次训练中成绩不低于10环的射击次数,
为本次训练中成绩不低于10环的射击次数, 的数学期望
的数学期望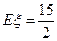 ,方差
,方差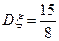 .
.
(1)求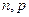 的值;
的值;
(2)训练中教练要求:若有5枪或5枪以上成绩低于10环,则需要补射,求该运动员在本次训练中需要补射的概率.
(结果用分数表示.已知: ,
,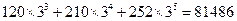 )
)