“勤劳”是中华民族的传统美德,学校要求同学们在家里帮助父母做一些力所能及的家务.在本学期开学初,小颖同学随机调查了部分同学寒假在家做家务的总时间,设被调查的每位同学寒假在家做家务的总时间为
小时,将做家务的总时间分为五个类别:
,
,
,
,
.并将调查结果制成如下两幅不完整的统计图:
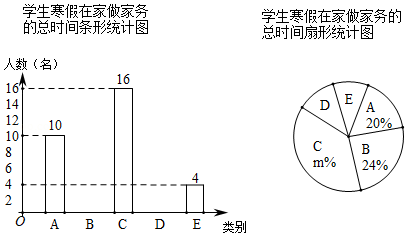
根据统计图提供的信息,解答下列问题:
(1)本次共调查了 名学生;
(2)请根据以上信息直接在答题卡中补全条形统计图;
(3)扇形统计图中
的值是 ,类别
所对应的扇形圆心角的度数是 度;
(4)若该校有800名学生,根据抽样调查的结果,请你估计该校有多少名学生寒假在家做家务的总时间不低于20小时.