在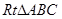 中,
中,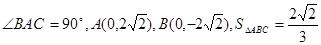 ,动点P的轨迹为曲线E,曲线E过点C且满足|PA|+|PB|为常数。
,动点P的轨迹为曲线E,曲线E过点C且满足|PA|+|PB|为常数。
(1)求曲线E的方程;
(2)是否存在直线L,使L与曲线E交于不同的两点M、N,且线段MN恰被直线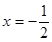 平分?若存在,求出L的斜率的取值范围;若不存在说明理由。
平分?若存在,求出L的斜率的取值范围;若不存在说明理由。
推荐套卷
在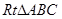 中,
中,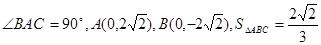 ,动点P的轨迹为曲线E,曲线E过点C且满足|PA|+|PB|为常数。
,动点P的轨迹为曲线E,曲线E过点C且满足|PA|+|PB|为常数。
(1)求曲线E的方程;
(2)是否存在直线L,使L与曲线E交于不同的两点M、N,且线段MN恰被直线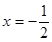 平分?若存在,求出L的斜率的取值范围;若不存在说明理由。
平分?若存在,求出L的斜率的取值范围;若不存在说明理由。