满足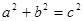 的三个正整数称为勾股数.
的三个正整数称为勾股数.
(1)下面是一种寻找勾股数组的方法:对任意两个正整数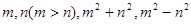 和
和 这三个数就是一组勾股数,请你验证这个结论.
这三个数就是一组勾股数,请你验证这个结论.
(2)以下是常见的几组勾股数:3,4,5; 5,12,13; 7,24,25; 8,15,17;
通过观察发现: 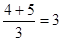 ;
;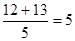 ;
;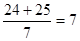 ;
; ,由此,某同学做出以下结论:在一组勾股数中,较大两个数的和能被最小的那个数整除.你认为他的结论正确吗?为什么?
,由此,某同学做出以下结论:在一组勾股数中,较大两个数的和能被最小的那个数整除.你认为他的结论正确吗?为什么?
相关知识点
推荐套卷
满足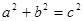 的三个正整数称为勾股数.
的三个正整数称为勾股数.
(1)下面是一种寻找勾股数组的方法:对任意两个正整数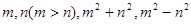 和
和 这三个数就是一组勾股数,请你验证这个结论.
这三个数就是一组勾股数,请你验证这个结论.
(2)以下是常见的几组勾股数:3,4,5; 5,12,13; 7,24,25; 8,15,17;
通过观察发现: 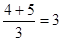 ;
;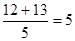 ;
;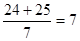 ;
; ,由此,某同学做出以下结论:在一组勾股数中,较大两个数的和能被最小的那个数整除.你认为他的结论正确吗?为什么?
,由此,某同学做出以下结论:在一组勾股数中,较大两个数的和能被最小的那个数整除.你认为他的结论正确吗?为什么?