已知抛物线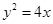
的焦点F，直线l过点
。
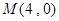（1）若点F到直线l的距离为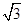
，求直线l的斜率；
（2）设A，B为抛物线上两点，且AB不与x轴垂直，若线段AB的垂直平分线恰过点M，求证：线段AB中点的横坐标为定值。
相关试题
，
，
在（0，4）上为单调函数，求
的取值范围．
为偶函数，曲线
过点
，
．
存在斜率为0的切线，求实数
的取值范围；
时函数
过点
，且与曲线
和
都相切，
的值。
是定义在R上的偶函数，其图象关于
对称，对任意的
，都有
，且
；
．
的图象过原点，且在原点处的切线斜率是
，求
的值；
上不单调，求
的取值范围．相关知识点
推荐套卷
已知抛物线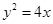的焦点F，直线l过点。
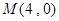（1）若点F到直线l的距离为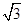，求直线l的斜率；
（2）设A，B为抛物线上两点，且AB不与x轴垂直，若线段AB的垂直平分线恰过点M，求证：线段AB中点的横坐标为定值。
粤公网安备 44130202000953号