如图，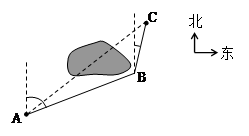
两岛之间有一片暗礁，一艘小船于某日上午8时从
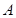岛出发，以10海里/小时的速度沿
北偏东75°方向直线航行，下午1时到达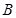
处.然后以同样的速度，沿北偏东 15°方向直线航
行，下午4时到达
岛.
（Ⅰ）求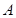、两岛之间的直线距离；
（Ⅱ）求
的正弦值.
，
在
上单调递减；
，求
的取值范围。
，且
的值；
的奇偶性；
于A，
于B，如果PA=10，AB=6，求
,
，且
.
的取值的集合；
时, 
恒成立,求实数
的取值范围.推荐套卷
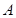如图，两岛之间有一片暗礁，一艘小船于某日上午8时从岛出发，以10海里/小时的速度沿
北偏东75°方向直线航行，下午1时到达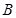处.然后以同样的速度，沿北偏东 15°方向直线航
行，下午4时到达岛.
（Ⅰ）求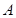、两岛之间的直线距离；
（Ⅱ）求的正弦值.
粤公网安备 44130202000953号