为了监控某种零件的一条生产线的生产过程,检验员每天从该生产线上随机抽取16个零件,并测量其尺寸(单位:cm).根据长期生产经验,可以认为这条生产线正常状态下生产的零件的尺寸服从正态分布
.
(1)假设生产状态正常,记 X表示一天内抽取的16个零件中其尺寸在
之外的零件数,求
及
的数学期望;
(2)一天内抽检零件中,如果出现了尺寸在
之外的零件,就认为这条生产线在这一天的生产过程可能出现了异常情况,需对当天的生产过程进行检查.
( ⅰ)试说明上述监控生产过程方法的合理性;
( ⅱ)下面是检验员在一天内抽取的16个零件的尺寸:
|
9.95 |
10.12 |
9.96 |
9.96 |
10.01 |
9.92 |
9.98 |
10.04 |
|
10.26 |
9.91 |
10.13 |
10.02 |
9.22 |
10.04 |
10.05 |
9.95 |
经计算得
,
,其中
为抽取的第
 个零件的尺寸,
.
个零件的尺寸,
.
用样本平均数
作为
的估计值
,用样本标准差
作为
的估计值
,利用估计值判断是否需对当天的生产过程进行检查?剔除
之外的数据,用剩下的数据估计
和
(精确到0.01).
附:若随机变量
服从正态分布
,则
,
,
.
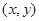 表示“甲在
表示“甲在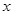 号车站下车,乙在
号车站下车,乙在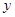 号车站下车”
号车站下车”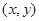 表示“甲在
表示“甲在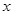 号车站下车,乙在
号车站下车,乙在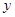 号车站下车”
号车站下车”