先阅读理解下面的例题,再按要求解答:
例题:解一元二次不等式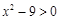 .
.
解:∵ ,
,
∴ .
.
由有理数的乘法法则“两数相乘,同号得正”,有
(1) (2)
(2)
解不等式组(1),得 ,
,
解不等式组(2),得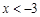 ,
,
故 的解集为
的解集为 或
或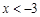 ,
,
即一元二次不等式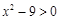 的解集为
的解集为 或
或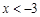 .
.
问题:⑴ 求关于x的两个多项式的商组成不等式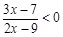 的解集;
的解集;
⑵ 若a,b是⑴中解集x的整数解,以a,b,c为△ABC为边长,c是△ABC中的最长的边长.
①求c的取值范围.
②若c为整数,求这个等腰△ABC的周长.
相关知识点
推荐套卷
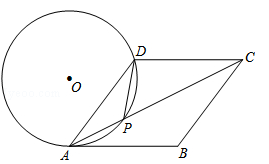
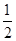 ,求⊙O的半径.
,求⊙O的半径. (即AB:BC=1:
(即AB:BC=1:
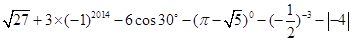 ;
;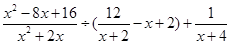 ,其中x为该不等式组
,其中x为该不等式组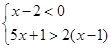 的整数解.
的整数解.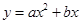 (
(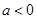 )的图象过坐标原点O,与x轴的负半轴交于点A,过A点的直线与y轴交于B,与二次函数的图象交于另一点C,且C点的横坐标为﹣1,AC:BC=3:1.
)的图象过坐标原点O,与x轴的负半轴交于点A,过A点的直线与y轴交于B,与二次函数的图象交于另一点C,且C点的横坐标为﹣1,AC:BC=3:1.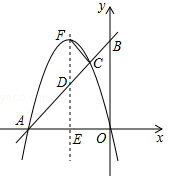
 粤公网安备 44130202000953号
粤公网安备 44130202000953号