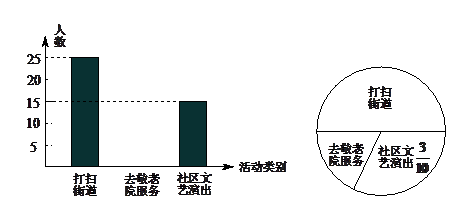今年3月5日,光明中学组织全体学生参加了“走出校门,服务社会”的活动,活动分为打扫街道、去敬老院服务和到社区文艺演出三项。从九年级参加活动的同学中抽取了部分同学对打扫街道、去敬老院服务和到社区文艺演出的人数进行了统计,并做了如下直方图和扇形统计图。请根据两个图形,回答以下问题:
(1)抽取的部分同学的人数?
(2)补全直方图的空缺部分.
(3)若九年级有400名学生,估计该年级去敬老院的人数.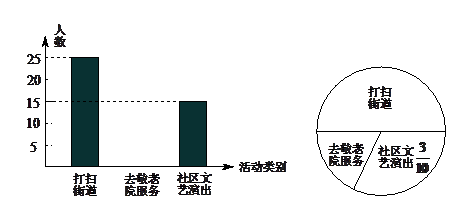
相关知识点
推荐套卷
今年3月5日,光明中学组织全体学生参加了“走出校门,服务社会”的活动,活动分为打扫街道、去敬老院服务和到社区文艺演出三项。从九年级参加活动的同学中抽取了部分同学对打扫街道、去敬老院服务和到社区文艺演出的人数进行了统计,并做了如下直方图和扇形统计图。请根据两个图形,回答以下问题:
(1)抽取的部分同学的人数?
(2)补全直方图的空缺部分.
(3)若九年级有400名学生,估计该年级去敬老院的人数.