已知：如图，在△ABC中，AB=AC，∠BAC=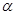
，且60°<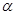<120°．P为△ABC内部一点，且PC=AC，∠PCA=120°—．
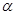（1）用含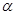的代数式表示∠APC，得∠APC =_______________________；
（2）求证：∠BAP=∠PCB；
（3）求∠PBC的度数．
.
，其中
，
（2）
＋
)(
。
，若
， 
，则
相关知识点
推荐套卷
已知：如图，在△ABC中，AB=AC，∠BAC=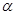，且60°<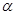<120°．P为△ABC内部一点，且PC=AC，∠PCA=120°—．
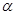（1）用含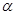的代数式表示∠APC，得∠APC =_______________________；
（2）求证：∠BAP=∠PCB；
（3）求∠PBC的度数．
粤公网安备 44130202000953号