如图,以△ABC的两边AB、AC向外作等边三角形ABE和等边三角形ACD,连结BD、CE,相交于O.(1)试写出图中和BD相等的一条线段并说明你的理由;(2)求出BD和CE的夹角大小,若改变△ABC的形状,这个夹角的度数会发生变化吗?请说明理由.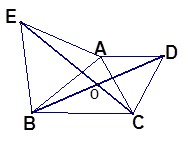
相关知识点
推荐套卷
如图,以△ABC的两边AB、AC向外作等边三角形ABE和等边三角形ACD,连结BD、CE,相交于O.(1)试写出图中和BD相等的一条线段并说明你的理由;(2)求出BD和CE的夹角大小,若改变△ABC的形状,这个夹角的度数会发生变化吗?请说明理由.