如图,已知Rt△ABC,AB=AC,∠ABC的平分线BD交AC于点D,BD的垂直平分线分别交AB,BC于点E、F,CD=CG。
(1)请以图中的点为顶点(不增加其他的点)分别构造两个菱形和两个等腰梯形。那么,构成菱形的四个顶点是__________或__________;构成等腰梯形的四个顶点是_____________或_____________.
(2)请你选择其中一个图形加以证明。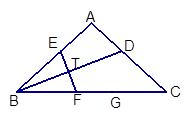
相关知识点
推荐套卷
如图,已知Rt△ABC,AB=AC,∠ABC的平分线BD交AC于点D,BD的垂直平分线分别交AB,BC于点E、F,CD=CG。
(1)请以图中的点为顶点(不增加其他的点)分别构造两个菱形和两个等腰梯形。那么,构成菱形的四个顶点是__________或__________;构成等腰梯形的四个顶点是_____________或_____________.
(2)请你选择其中一个图形加以证明。