如图,在所给网格图(每小格均为边长是1的正方形)中完成下列各题:
(1)在下图中画出格点△ABC(顶点均在格点上)关于直线DE对称的△A1B1C1;
(2)以AB所在的直线为x轴、DE所在的直线为y轴建立直角坐标系xoy,并直接写出在此坐标系下A1B1C1的坐标;
(3)求出△ABC的面积。
(2) A1( ), B1( ), C1( )
(3)S△ABC=_____________________
相关知识点
推荐套卷
 ,
,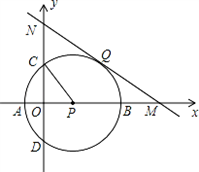
 为⊙
为⊙ 的直径,
的直径, 与⊙
与⊙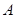 ,
,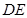 与⊙
与⊙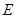 ,点
,点 为
为
 为⊙
为⊙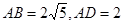 ,求线段BC的长.
,求线段BC的长. .
.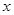 ,然后由小强再随机摸出一个球记为
,然后由小强再随机摸出一个球记为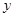 .小明和小强在此基础上共同协商一个游戏规则:当
.小明和小强在此基础上共同协商一个游戏规则:当 粤公网安备 44130202000953号
粤公网安备 44130202000953号