甲，乙两人进行乒乓球比赛，约定每局胜者得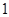
分，负者得
分，比赛进行到有一人比对方多
分或打满
局时停止．设甲在每局中获胜的概率为
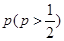，且各局胜负相互独立．已知第二局比赛结束时比赛停止的概率为
．
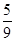（Ⅰ）求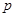
的值；
（Ⅱ）设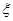
表示比赛停止时比赛的局数，求随机变量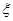的分布列和数学期望
．
，
，试用
表示
。 
两两所成的角相等，且
，求
。
，求： 
的值；（2）
的值．
,
,且
及
;
的最小值
.
，其中
.
的取值范围；
的大小
的最小正周期；
，求
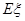的值。相关知识点
推荐套卷
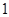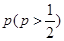甲，乙两人进行乒乓球比赛，约定每局胜者得分，负者得分，比赛进行到有一人比对方多分或打满局时停止．设甲在每局中获胜的概率为，且各局胜负相互独立．已知第二局比赛结束时比赛停止的概率为．
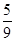（Ⅰ）求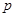的值；
（Ⅱ）设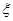表示比赛停止时比赛的局数，求随机变量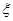的分布列和数学期望．
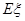粤公网安备 44130202000953号