甲、乙两同学进行投篮比赛，每一局每人各投两次球，规定进球数多者该局获胜，进球数相同则为平局.已知甲每次投进的概率为
，乙每次投进的概率为
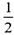，甲、乙之间的投篮相互独立.
(1) 求一局比赛甲进两球获胜的概率；
(2) 求一局比赛的结果不是平局的概率.
相关试题
，
的顶点是该双曲线的中心，而焦点是其左顶点，求抛物线
，函数
。
均有
是
的充分条件；
时，求
恒成立的充要条件。
.求复数z1及它的模| z2|．
是等差数列，
，公差
，求证：
推荐套卷
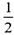甲、乙两同学进行投篮比赛，每一局每人各投两次球，规定进球数多者该局获胜，进球数相同则为平局.已知甲每次投进的概率为，乙每次投进的概率为，甲、乙之间的投篮相互独立.
(1) 求一局比赛甲进两球获胜的概率；
(2) 求一局比赛的结果不是平局的概率.
粤公网安备 44130202000953号