如图，山坡上有一棵树AB，树底部B点到山脚C点的距离BC为
米，山坡的坡角为30°．小宁在山脚的平地F处测量这棵树的高，点C到测角仪EF的水平距离CF=1米，从E处测得树顶部A的仰角为45°，树底部B的仰角为20°，求树AB的高度．（参考数值：sin20°≈0.34，cos20°≈0.94，tan20°≈0.36）
相关试题
（2）
（2）
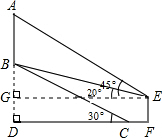
相关知识点
推荐套卷
如图，山坡上有一棵树AB，树底部B点到山脚C点的距离BC为米，山坡的坡角为30°．小宁在山脚的平地F处测量这棵树的高，点C到测角仪EF的水平距离CF=1米，从E处测得树顶部A的仰角为45°，树底部B的仰角为20°，求树AB的高度．（参考数值：sin20°≈0.34，cos20°≈0.94，tan20°≈0.36）
粤公网安备 44130202000953号