已知函数 .
.
(Ⅰ)当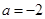 时,求函数
时,求函数 的单调区间;
的单调区间;
(Ⅱ)是否存在实数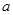 ,使得函数
,使得函数 有唯一的极值,且极值大于
有唯一的极值,且极值大于 ?若存在,,求
?若存在,,求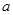 的取值
的取值
范围;若不存在,说明理由;
(Ⅲ)如果对 ,总有
,总有 ,则称
,则称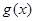 是
是 的凸
的凸
函数,如果对 ,总有
,总有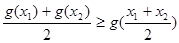 ,则称
,则称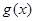 是
是 的凹函数.当
的凹函数.当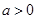 时,利用定义分析
时,利用定义分析 的凹凸性,并加以证明。
的凹凸性,并加以证明。
推荐套卷
已知函数 .
.
(Ⅰ)当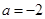 时,求函数
时,求函数 的单调区间;
的单调区间;
(Ⅱ)是否存在实数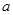 ,使得函数
,使得函数 有唯一的极值,且极值大于
有唯一的极值,且极值大于 ?若存在,,求
?若存在,,求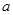 的取值
的取值
范围;若不存在,说明理由;
(Ⅲ)如果对 ,总有
,总有 ,则称
,则称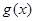 是
是 的凸
的凸
函数,如果对 ,总有
,总有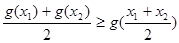 ,则称
,则称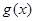 是
是 的凹函数.当
的凹函数.当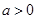 时,利用定义分析
时,利用定义分析 的凹凸性,并加以证明。
的凹凸性,并加以证明。