(本小题满分12分)
为了加快经济的发展,某市选择A、B两区作为龙头带动周边地区的发展,决定在A、B两区的周边修建城际快速通道,假设A、B两区相距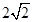 个单位距离,城际快速通道所在的曲线为E,使快速通道E上的点到两区的距离之和为4个单位距离.
个单位距离,城际快速通道所在的曲线为E,使快速通道E上的点到两区的距离之和为4个单位距离.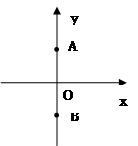
(Ⅰ)以线段AB的中点O为原点建立如图所示的直角坐标系,求城际快速通道所在曲线E的方程;
(Ⅱ)若有一条斜率为 的笔直公路l与曲线E交于P,Q两点,同时在曲线E上建一个加油站M(横坐标为负值)满足
的笔直公路l与曲线E交于P,Q两点,同时在曲线E上建一个加油站M(横坐标为负值)满足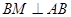 ,求
,求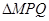 面积的最大值.
面积的最大值.
推荐套卷
 .
. ,sin
,sin ,sin
,sin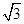 .
.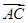 |+|
|+| |=
|= |,试判断△ABC的形状.
|,试判断△ABC的形状. ,-1).
,-1). =
= +t
+t ,试问:
,试问: 粤公网安备 44130202000953号
粤公网安备 44130202000953号