（本小题满分12分）
在边长为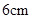
的正方形ABCD中，E、F分别为BC、CD的中点，M、N分别为AB、CF的中点，现沿AE、AF、EF折叠，使B、C、D三点重合于B，构成一个三棱锥(如图所示)．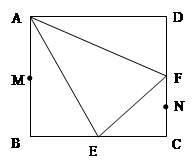
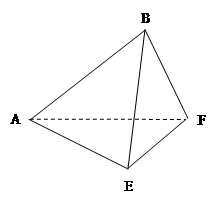
（Ⅰ）在三棱锥上标注出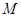
、
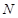点，并判别MN与平面AEF的位置关系，并给出证明；
（Ⅱ）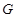
是线段
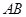上一点，且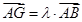
, 问是否存在点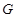使得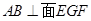
,若存在，求出
的值;若不存在，请说明理由；
（Ⅲ）求多面体E-AFNM的体积．
的定义域
的值。
的值。
，判断其函数的奇偶性。
}，N={
}，求
的值推荐套卷
（本小题满分12分）
在边长为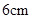的正方形ABCD中，E、F分别为BC、CD的中点，M、N分别为AB、CF的中点，现沿AE、AF、EF折叠，使B、C、D三点重合于B，构成一个三棱锥(如图所示)．
（Ⅰ）在三棱锥上标注出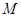、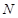点，并判别MN与平面AEF的位置关系，并给出证明；
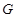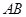（Ⅱ）是线段上一点，且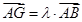, 问是否存在点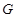使得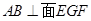,若存在，求出的值;若不存在，请说明理由；
（Ⅲ）求多面体E-AFNM的体积．
粤公网安备 44130202000953号