学校为了调查学生对教学的满意度，随机抽取了部分学生作问卷调查：用“A”表示“很满意“，“B”表示“满意”，“C”表示“比较满意”，“D”表示“不满意”，如图甲、乙是工作人员根据问卷调查统计资料绘制的两幅不完整的统计图，请你根据统计图提供的信息解答以下问题：
（1）本次问卷调查，共调查了多少名学生？
（2）将图甲中“B”部分的图形补充完整；
（3）如果该校有学生1000人，请你估计该校学生对教学感到“不满意”的约有多少人？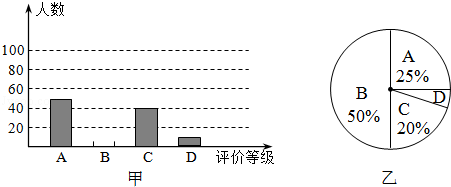
相关试题
一个不透明的口袋中有三个小球，上面分别标有字母，
，
，除所标字母不同外，其它完全相同，从中随机摸出一个小球，记下字母后放回并搅匀，再随机摸出一个小球，用画树状图（或列表）的方法，求该同学两次摸出的小球所标字母相同的概率．
某同学化简出现了错误，解答过程如下：
原式 （第一步）
（第二步）
（第三步）
（1）该同学解答过程从第 步开始出错，错误原因是 ；
（2）写出此题正确的解答过程．
相关知识点
推荐套卷
粤公网安备 44130202000953号