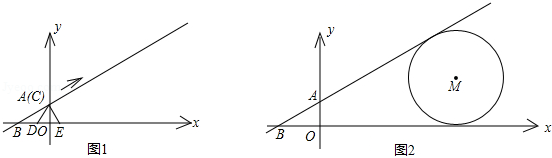如图，在平面直角坐标系中，直线y=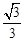
x+1分别与两坐标轴交于B，A两点，C为该直线上的一动点，以每秒1个单位长度的速度从点A开始沿直线BA向上移动，作等边△CDE，点D和点E都在x轴上，以点C为顶点的抛物线y=a（x﹣m）2+n经过点E．⊙M与x轴、直线AB都相切，其半径为3（1﹣
）a．
（1）求点A的坐标和∠ABO的度数；
（2）当点C与点A重合时，求a的值；
（3）点C移动多少秒时，等边△CDE的边CE第一次与⊙M相切？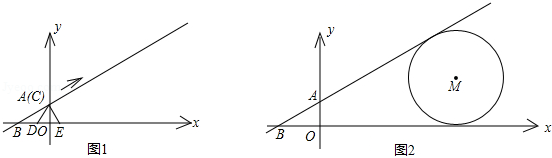
的差等于48的
是方程x－6y+16=0的解，则t=?
是方程2x－6my+8=0的一组解，求m的值.相关知识点
推荐套卷
如图，在平面直角坐标系中，直线y=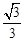x+1分别与两坐标轴交于B，A两点，C为该直线上的一动点，以每秒1个单位长度的速度从点A开始沿直线BA向上移动，作等边△CDE，点D和点E都在x轴上，以点C为顶点的抛物线y=a（x﹣m）2+n经过点E．⊙M与x轴、直线AB都相切，其半径为3（1﹣）a．
（1）求点A的坐标和∠ABO的度数；
（2）当点C与点A重合时，求a的值；
（3）点C移动多少秒时，等边△CDE的边CE第一次与⊙M相切？
粤公网安备 44130202000953号