如图1，△ABC内接于半径为4cm的⊙O，AB为直径，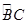
长为
．
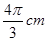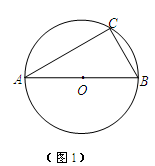
（1）计算∠ABC的度数；
（2）将与△ABC全等的△FED如图2摆放，使两个三角形的对应边DF与AC有一部分重叠，△FED的最长边EF恰好经过
的中点M．求证：AF=AB；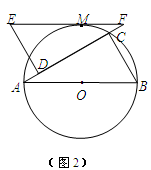
（3）设图2中以A、C、M为顶点的三角形面积为S，求出S的值．
相关知识点
推荐套卷
如图1，△ABC内接于半径为4cm的⊙O，AB为直径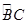，长为．
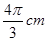（1）计算∠ABC的度数；
（2）将与△ABC全等的△FED如图2摆放，使两个三角形的对应边DF与AC有一部分重叠，△FED的最长边EF恰好经过的中点M．求证：AF=AB；
（3）设图2中以A、C、M为顶点的三角形面积为S，求出S的值．
粤公网安备 44130202000953号