(本小题满分11分)(注意:在试题卷上作答无效)
已知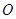 为坐标原点,向量
为坐标原点,向量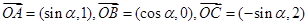 ,点
,点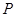 是直线
是直线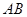 上的一点,且点
上的一点,且点 分有向线段
分有向线段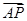 的比为
的比为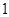 .
.
(1)记函数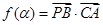 ,
,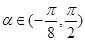 ,讨论函数
,讨论函数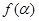 的单调性,并求其值域;
的单调性,并求其值域;
(2)若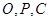 三点共线,求
三点共线,求 的值.
的值.
相关知识点
推荐套卷
(本小题满分11分)(注意:在试题卷上作答无效)
已知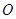 为坐标原点,向量
为坐标原点,向量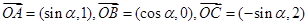 ,点
,点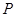 是直线
是直线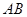 上的一点,且点
上的一点,且点 分有向线段
分有向线段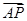 的比为
的比为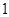 .
.
(1)记函数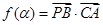 ,
,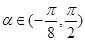 ,讨论函数
,讨论函数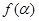 的单调性,并求其值域;
的单调性,并求其值域;
(2)若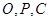 三点共线,求
三点共线,求 的值.
的值.