（本小题满分12分）
在四棱锥P－ABCD中，∠ABC＝∠ACD＝90°，∠BAC＝∠CAD＝60°，PA⊥平面ABCD，E为PD的中点，PA＝2AB＝2．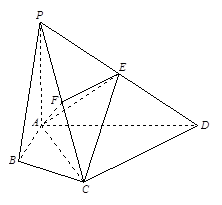
（Ⅰ）求四棱锥P－ABCD的体积V；
（Ⅱ）若F为PC的中点，求证PC⊥平面AEF；
相关试题
.
的值．
＋lg 7－lg 18；
－
；
＋
的值．推荐套卷
（本小题满分12分）
在四棱锥P－ABCD中，∠ABC＝∠ACD＝90°，∠BAC＝∠CAD＝60°，PA⊥平面ABCD，E为PD的中点，PA＝2AB＝2．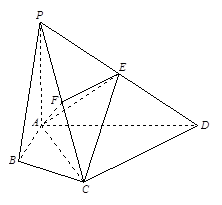
（Ⅰ）求四棱锥P－ABCD的体积V；
（Ⅱ）若F为PC的中点，求证PC⊥平面AEF；
粤公网安备 44130202000953号