顶点在坐标原点,开口向上的抛物线经过点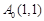 ,过点
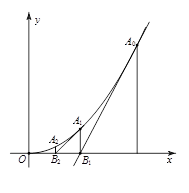
,过点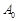 作抛物线的切线交x轴于点B1,过点B1作x轴的垂线交抛物线于点A1,过点A1作抛物线的切线交x轴于点B2,…,过点
作抛物线的切线交x轴于点B1,过点B1作x轴的垂线交抛物线于点A1,过点A1作抛物线的切线交x轴于点B2,…,过点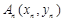 作抛物线的切线交x轴于点
作抛物线的切线交x轴于点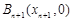 .
.
(1)求数列{ xn },{ yn}的通项公式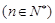 ;
;
(2)设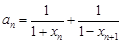 ,数列{ an}的前n项和为Tn.求证:
,数列{ an}的前n项和为Tn.求证: ;
;
(3)设 ,若对于任意正整数n,不等式
,若对于任意正整数n,不等式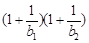 …
…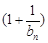 ≥
≥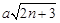 成立,求正数a的取值范围.
成立,求正数a的取值范围.
推荐套卷
顶点在坐标原点,开口向上的抛物线经过点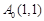 ,过点
,过点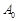 作抛物线的切线交x轴于点B1,过点B1作x轴的垂线交抛物线于点A1,过点A1作抛物线的切线交x轴于点B2,…,过点
作抛物线的切线交x轴于点B1,过点B1作x轴的垂线交抛物线于点A1,过点A1作抛物线的切线交x轴于点B2,…,过点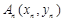 作抛物线的切线交x轴于点
作抛物线的切线交x轴于点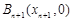 .
.
(1)求数列{ xn },{ yn}的通项公式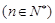 ;
;
(2)设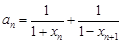 ,数列{ an}的前n项和为Tn.求证:
,数列{ an}的前n项和为Tn.求证: ;
;
(3)设 ,若对于任意正整数n,不等式
,若对于任意正整数n,不等式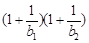 …
…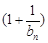 ≥
≥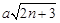 成立,求正数a的取值范围.
成立,求正数a的取值范围.