在一个可以改变体积的容器内有一定质量的二氧化碳气体,当改变容器的体积时,气体的密度也会随之改变,密度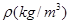 与体积
与体积
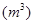 之间的函数关系如图所示。
之间的函数关系如图所示。
(1)通过图象你能得到什么信息(至少写一条)?
(2)写出 与
与 之间函数关系式;
之间函数关系式;
(3)求当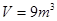 时,二氧化碳的密度
时,二氧化碳的密度 。
。
相关知识点
推荐套卷
在一个可以改变体积的容器内有一定质量的二氧化碳气体,当改变容器的体积时,气体的密度也会随之改变,密度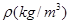 与体积
与体积
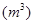 之间的函数关系如图所示。
之间的函数关系如图所示。
(1)通过图象你能得到什么信息(至少写一条)?
(2)写出 与
与 之间函数关系式;
之间函数关系式;
(3)求当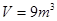 时,二氧化碳的密度
时,二氧化碳的密度 。
。