如图1,在第一象限内,直线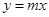 与过点
与过点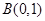 且平行于
且平行于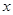 轴的直线
轴的直线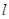 相交于点
相交于点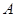 ,半径为
,半径为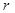 的⊙
的⊙ 与直线
与直线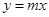 、
、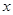 轴分别相切于点
轴分别相切于点 、
、 ,且与直线
,且与直线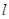 分别交于不同的
分别交于不同的 、
、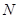 两点.
两点.
(1)当点A的坐标为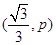 时,
时,
① 填空: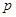 = ,
= ,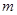 = ,
= ,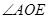 = ;
= ;
②如图2,连结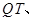
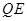 ,
,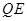 交直线
交直线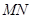 于
于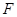 ,当
,当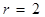 时,试说明以
时,试说明以 、
、  、
、 、
、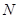 为顶点的四边形是等腰梯形;
为顶点的四边形是等腰梯形;
(2)在图1中,连结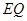 并延长交⊙
并延长交⊙ 于点
于点 ,试探索:对不同的
,试探索:对不同的 取值,经过
取值,经过 、
、 、
、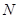 三点的抛物线
三点的抛物线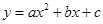 ,
,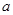 的值会变化吗?若不变,求出
的值会变化吗?若不变,求出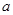 的值;若变化,请说明理由.
的值;若变化,请说明理由.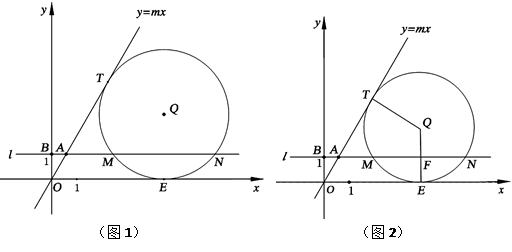
相关知识点
推荐套卷

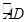 =
=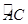 ,弦AB与弦AC交于点A,弦CD与AB交于点F,连接BC.
,弦AB与弦AC交于点A,弦CD与AB交于点F,连接BC.

 ≈1.41,
≈1.41, ≈1.73)
≈1.73)
 ≈1.41,
≈1.41, ≈1.73,
≈1.73, =2.45).
=2.45).
 粤公网安备 44130202000953号
粤公网安备 44130202000953号