为了探索代数式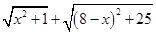 的最小值,小明巧妙的运用了“数形结合”思想.具体方法是这样的:如图,C为线段BD上一动点,分别过点B、D作
的最小值,小明巧妙的运用了“数形结合”思想.具体方法是这样的:如图,C为线段BD上一动点,分别过点B、D作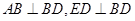 ,连结AC、EC.已知AB=1,DE=5,BD=8,设BC=x.则
,连结AC、EC.已知AB=1,DE=5,BD=8,设BC=x.则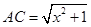 ,
,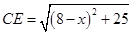 则问题即转化成求AC+CE的最小值.
则问题即转化成求AC+CE的最小值.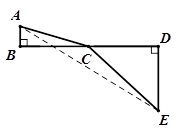
(1)我们知道当A、C、E在同一直线上时, AC+CE的值最小,于是可求得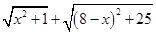 的最小值等于 ,此时
的最小值等于 ,此时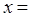 ;
;
(2)请你根据上述的方法和结论,试构图求出代数式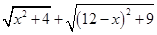 的最小值.
的最小值.
相关知识点
推荐套卷
为了探索代数式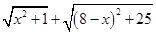 的最小值,小明巧妙的运用了“数形结合”思想.具体方法是这样的:如图,C为线段BD上一动点,分别过点B、D作
的最小值,小明巧妙的运用了“数形结合”思想.具体方法是这样的:如图,C为线段BD上一动点,分别过点B、D作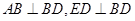 ,连结AC、EC.已知AB=1,DE=5,BD=8,设BC=x.则
,连结AC、EC.已知AB=1,DE=5,BD=8,设BC=x.则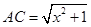 ,
,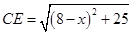 则问题即转化成求AC+CE的最小值.
则问题即转化成求AC+CE的最小值.
(1)我们知道当A、C、E在同一直线上时, AC+CE的值最小,于是可求得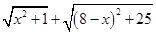 的最小值等于 ,此时
的最小值等于 ,此时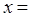 ;
;
(2)请你根据上述的方法和结论,试构图求出代数式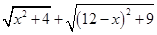 的最小值.
的最小值.