某区在实施居民用水额定管理前,对居民生活用水情况进行了调查,下表是通过简单随机抽样获得的50个家庭去年的月均用水量(单位:吨),并将调查数据进行了如下整理:
4.7 2.1 3.1 2.3 5.2 2.8 7.3 4.3 4.8 6.7
4.5 5.1 6.5 8.9 2.2 4.5 3.2 3.2 4.5 3.5
3.5 3.5 3.6 4.9 3.7 3.8 5.6 5.5 5.9 6.2
5.7 3.9 4.0 4.0 7.0 3.7 9.5 4.2 6.4 3.5
4.5 4.5 4.6 5.4 5.6 6.6 5.8 4.5 6.2 7.5
列频数分布表:
分组
|
划记
|
频数
|
2.0<x≤3.5
|
正正一
|
11
|
3.5<x≤5.0
|
正正正止
|
19
|
5.0<x≤6.5
|
|
|
6.5<x≤8.0
|
|
|
8.0<x≤9.5
|
ㄒ
|
2
|
合计
|

|
50
|
画频数分布直方图:
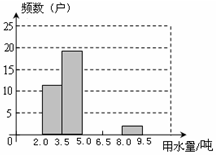
(1)把上面的频数分布表和频数分布直方图补充完整;
(2)从直方图中你能得到什么信息?(写出两条即可)
(3)为了鼓励节约用水,要确定一个用水量的标准,超出这个标准的部分按1.5倍价格收费.若要使60%的家庭收费不受影响,你觉得家庭月均用水量应该定为多少?为什么?


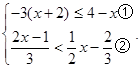 并求它的所有整数解.
并求它的所有整数解.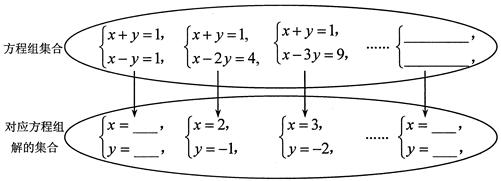
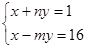 的解是
的解是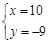 ,求m、n的值,并判断该方程组是否符合(2)中的规律?
,求m、n的值,并判断该方程组是否符合(2)中的规律? ;
; ,试求方程中的
,试求方程中的 值.
值. 粤公网安备 44130202000953号
粤公网安备 44130202000953号