(本小题满分12分)某校高二年级有500名学生,为了了解数学学科的学习情况,现从中随机抽出若干名学生在一次测试中的数学成绩,制成如下频率分布表:
分组
|
频数
|
频率
|
[85,95)
|
①
|
②
|
[95,105)
|
|
0.050
|
[105,115)
|
|
0.200
|
[115,125)
|
12
|
0.300
|
[125,135)
|
|
0.275
|
[135,145)
|
4
|
③
|
[145,155)
|
|
0.050
|
合计
|
|
④
|
(1)根据上面图表,①②③④处的数值分别为________、________、________、________;
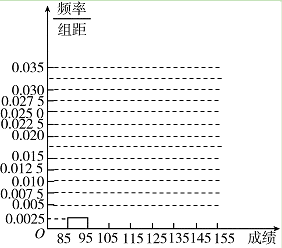
(2)在所给的坐标系中画出[85,155]的频率分布直方图;
(3)根据题中信息估计总体平均数,并估计总体落在[129,155]中的频率.